“You know, Valentine’s Day reminds me of the optimal stopping problem.” Not sure if this phrase was uttered elsewhere, but, this is the sort of water cooler conversations at Lumina HQ. I had a recent conversation about the (somewhat old fashioned in name) secretary problem, and agree that app-driven dating is a decision problem well suited to the application of optimal stopping theory! Care of Professor Thomas Ferguson, optimal stopping concerns itself with “the problem of choosing a time to take a given action based on sequentially observed random variables in order to maximize an expected payoff or to minimize an expected cost”. In our case, that choice is a Valentine’s date.
(If the distillation of a human being into a single score necessary for the purposes of this exercise is distasteful to you, please picture Tudder instead of Tinder. Cows can now participate in #swipelife – what a world!)
I built a simple Analytica simulation to explore the optimal stopping in selecting an optimal Valentine’s date. You can download the model here, and run it in the free edition of Analytica! I model a situation where you have 100 candidates. You swipe left 37 times (100/e) to figure out the best candidate of that bunch, and will swipe right on the first one you see who is better than the best in that learning set (or the 100th candidate, if nobody passes that test).
The model results over 100 simulations:
• 38% of the time, you will pick the single best (best single?) candidate — this is as expected
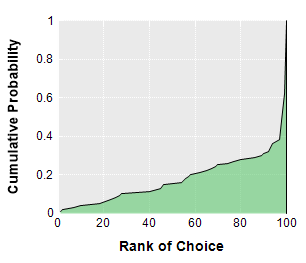
• 64% of the time, you’ll swipe right on a great candidate (top 5% in my model); the rest of the time, you’ll pick whomever was last in line so as not to have no date (cow) at all. You’ll see in the left figure below, you have ~uniform odds of picking any rank until you hit a rank above the top 10%.
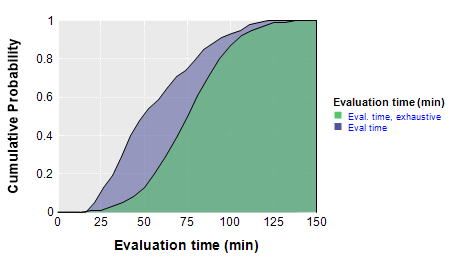
• You’ll spend 27% less time making this decision than if you evaluated all 100 candidates. The right figure below illustrates this savings.
I like this example topic because, at its core, its about reducing stress and time when making a decision. You have made a rational choice in matching the method to decision problem, and ideally feel neither FOMO (fear of missing out) nor FOBO (fear of better options) because you know you made a great choice! And since this was framed as the Valentine’s Date Problem and not the Marriage Problem, you can try for a better outcome next Friday night if the candidate you picked wasn’t the one.






