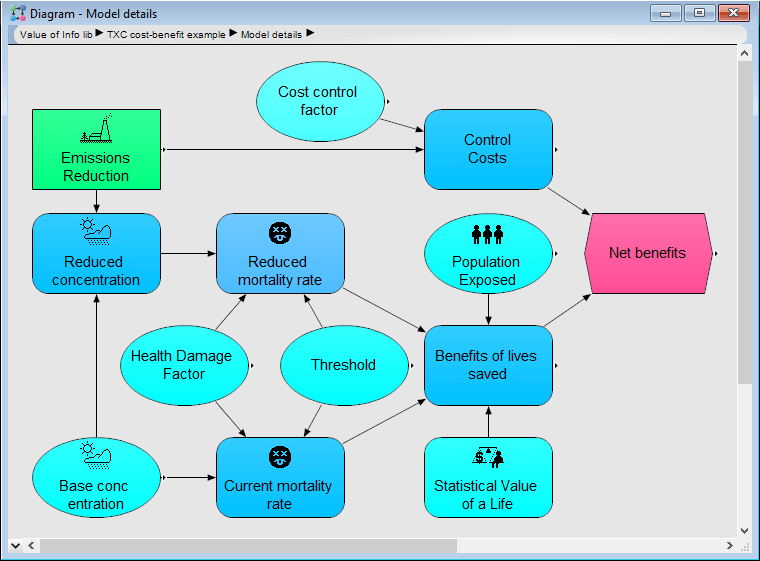
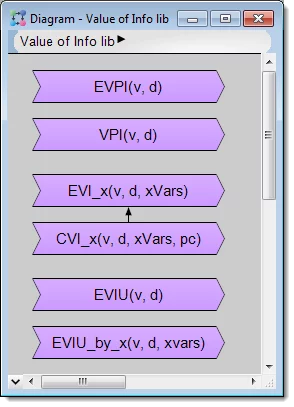
The expected value of information (EVI) lets you estimate the value of getting new information that reduces uncertainty. At first blush, it seems paradoxical that you can estimate the value of information about an uncertain quantity X before you find out the information – e.g. the actual value of X. The key is that it’s the expected value of information – i.e. the increase in value due to making your decision after you learn the value of X, taking the expectation (or average) over your current uncertainty in X expressed as a probability distribution. Some people use the shorter ”value of information” or just ”VOI”. I prefer the full ”expected value of information” (”EVI”) to remind us that the value is ”expected” – i.e. taking the mean over a probability distribution.
EVI as the most powerful tool for sensitivity analysis
The EVI is arguably the most sophisticated and powerful method for sensitivity analysis. It is a global sensitivity method – meaning that it estimates the effect of each variable averaging (taking conditional expectation) over the other uncertain variables – rather than the simpler but sometimes misleading local methods, like range sensitivity or Tornado charts, that look at each sensitivity assuming all other variables are fixed at a base value. EVI doesn’t just answer the question of how much difference it would make to your output value. It tells you the increase in expected value due to the decision maker making a better decision based on the information. As a decision analyst, that’s what you should really care about when thinking about sensitivity.
Formulating as a decision analysis
This power comes with some assumptions: To use EVI, you must formulate your model as a decision analysis – that is, with an explicit objective, decisions, and chance variables with uncertainty is expressed using probability distributions. It also assumes that the decision maker will select a decision that maximizes expected value (or utility) according to the specified objective – whether before or after getting the new information.
Efficient estimation of EVI
There has long been debate among decision analysts about whether it’s better to use discrete decision trees instead of Monte Carlo simulation or Latin hypercube sampling. With decision trees, you must approximate each continuous chance variable by a few discrete values – typically 3 to 5 – instead of treating it as continuous. One argument for discrete decision trees has been that it is impossible or, at least, computationally intractable, to estimate the EVI using simulation methods, since it requires M2 evaluations, where M is the Monte Carlo sample size. Actually, this is a misconception. It’s quite practical to estimate EVI using sampling methods. I’ve just added an Analytica library so you can apply it to your own decision models.
Value of information library.ana.
To estimate the expected value of perfect information (EVPI) that resolves all uncertainties, the complexity – i.e. the number of times you need to evaluate the model – is 2 * Nd * M, where Nd is the number of decision options, and M is the number of Monte Carlo or Latin hypercube samples.
In practice, it’s usually more useful to estimate the EVI for information separately for each uncertain variable Xi, (for i = 1 to Nx) in your model. The Analytica function EVI_x(v, d, Xi, Pc) takes Nd * (Nx + 1) * Nc * M evaluations, where Nc is the number of values for each uncertain quantity Xi. Typically, Nc = 10 to 20 is quite adequate, using Latin hypercube sampling. Note that EVI is a rough guide to sensitivity, like any measure of sensitivity, and a relatively small sample size of say 100 to 1000 is usually more than adequate. In cases with long-tailed distributions on value – e.g. with low probability high-consequence events – like a major accident or windfall – you can use importance sampling to oversample the rare events and get good results with a modest sample size.
For more, and to download the EVI library with or without examples, visit the EVI wiki page.