Image source: adcats.et.byu.edu
The use of random numbers as input is a defining feature of Monte Carlo simulations. This is what turns a deterministic model into a stochastic one, although how those random numbers are generated in the first place also affects the way the simulation runs. A Monte Carlo simulation lets you see how uncertainty is propagated, and how the performance, reliability and sensitivity of a model are affected by lack of knowledge or random variations.
Where should you get your random numbers?
What is random? People have tried different methods for generating random numbers such as ‘least significant digits’ in measures of time. Mathematical functions exist that generate sequences of numbers that look like random numbers: these are called pseudo-random numbers. Starting off with a ‘seed value’ generates a particular sequence, and using a different seed value gives another sequence. This has two effects. The first is that different seed values need to be used, or the Monte Carlo simulation will continually give the same result. However, the second is that by recording the seed values used, the simulation becomes reproducible – an important point in correcting and refining the simulation.
Making it reproducible
Scientific experiments, organizational audits and Monte Carlo simulations have certain things in common: they should be impartial, systematic and reproducible. Sources of error need to be controllable or at least isolatable. Then the basic steps of conducting a Monte Carlo simulation can be followed:
- Create a model with appropriate parameters
- Generate datasets of random numbers as inputs (one number per parameter per dataset)
- Run the simulation and record the result for each dataset
- Analyze the results with statistical tools such as confidence intervals.
Image source: vertex42.com
From what you know about real-life inputs into the system you want to simulate, choose the probability distribution for the inputs that comes closest to that observed in reality.
Image source: fda.gov
Variables and variations on a Monte Carlo theme
Von Neumann, one of the first to work with Monte Carlo simulations, used pseudo-random numbers. He found that if the simulation then went wrong, it did so in an obvious way, making it easier to identify possible problems. In some financial applications, Quasi Monte Carlo simulations are found to work better. In these simulations, random numbers are replaced by ‘low-discrepancy’ sequences (‘quasi-random’ sequences). In sports contexts and betting, Monte Carlo simulations have also been used to model separate events like football matches, and then combine the results to achieve a forecast of results that spans a complete football season. Similar approaches could be used to model larger events such as earthquakes affecting industrial facilities.
Don’t stop if or when you get a desired outcome
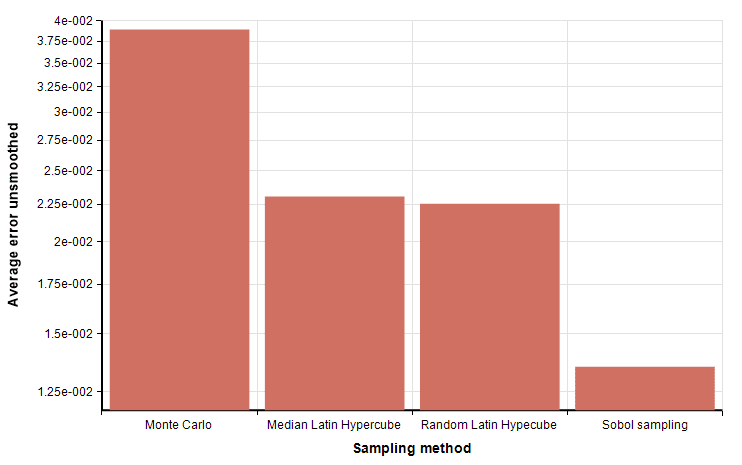
It may be tempting to call a halt to a Monte Carlo simulation when the output is something you suspected should be the result. This temptation can be resisted by making sure the simulation is run a statistically significant number of times, checked by, and even preferably performed by an independent entity. In addition, error in Monte Carlo simulations has been shown to change in the ration of 1/(square root of M), where M is the number of sample points. It’s better therefore to define an appropriate value for M (perhaps 10,000), run the simulation and average the results to reach an objective result with correspondingly less chance of error.
If you’d like to know how Analytica, the modeling software from Lumina, can help you to model uncertainty in Monte Carlo simulations, then try Analytica for free to see what it can do for you.