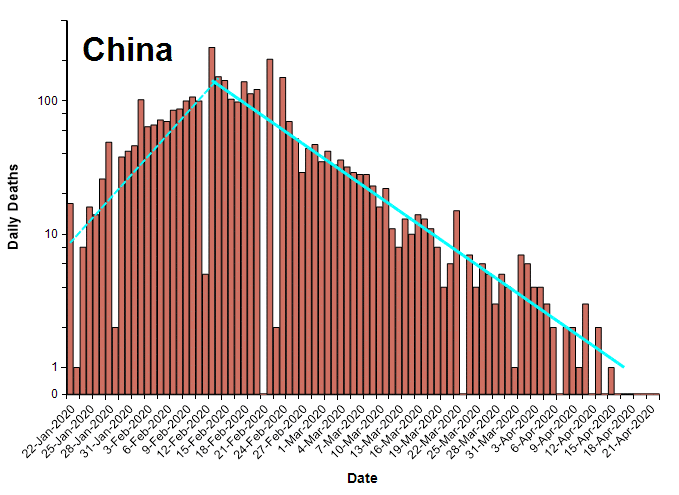
In previous articles [C20a, H20], my colleague and I have written about how the number of cases and deaths from COVID-19 follows a triangle shape over time when plotted with a log-scaled Y axis. A log-Y axis turns exponential growth into a straight line with a positive slope and exponential decay into a straight line with a negative slope. The negative slope results from the effects of social distancing measures. There is a roughly three week time lag between the introduction of lock down measures to the peak of the daily deaths curve, due to the fact that people who just caught the disease when social distancing starts and will eventually die from it, typically die about three weeks later.
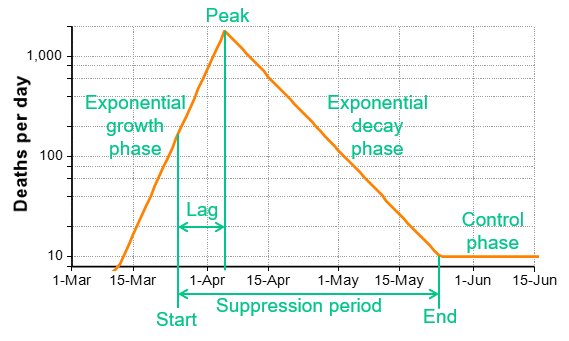
A key prediction of the Triangle Suppression model is that the decay phase is likely to be slower than the growth phase. In China, the decay during recovery was slower the growth phase by a factor of two. For the rest of the world where only less extreme lock downs are possible, the model predicts that the recovery will occur more slowly. In [C20b], I critiqued the IMHE model [IMHE20] from HealthData.org, where my largest concern was the assumption that recovery will occur at the same rate as growth, which underestimates the length of the recovery time relative to the Triangle Suppression model.
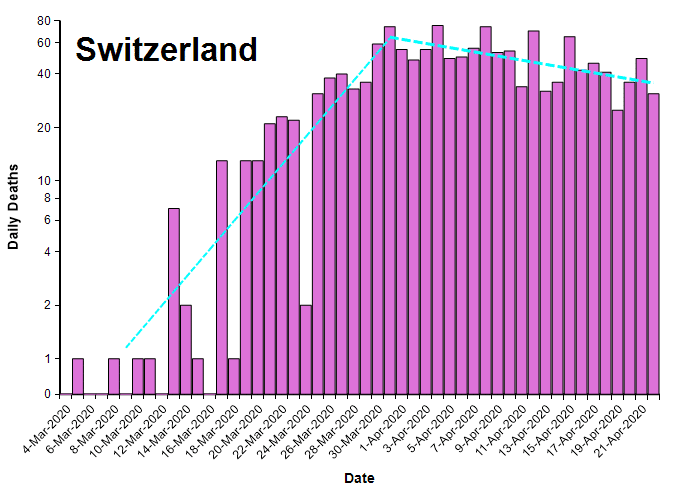
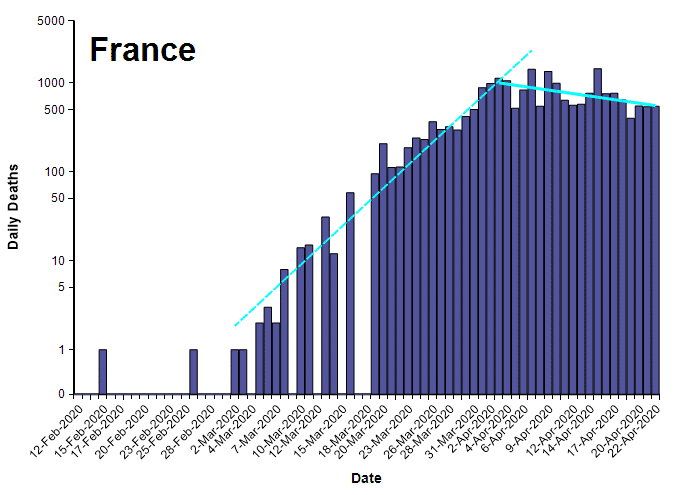
A few countries appear to have crossed a peak, with just enough data to get a preliminary reading of their decay rates. In this article, I share these graphs, and look at the ratio of growth rate to decay rate for these countries.
Daily deaths
The plots in this section show the number of deaths per day from COVID-19 (from the John Hopkins data set [JH20]) for several countries that seem to have crossed a peak, plotted on a log-Y axis. Exponential growth and decay lines are super-imposed.
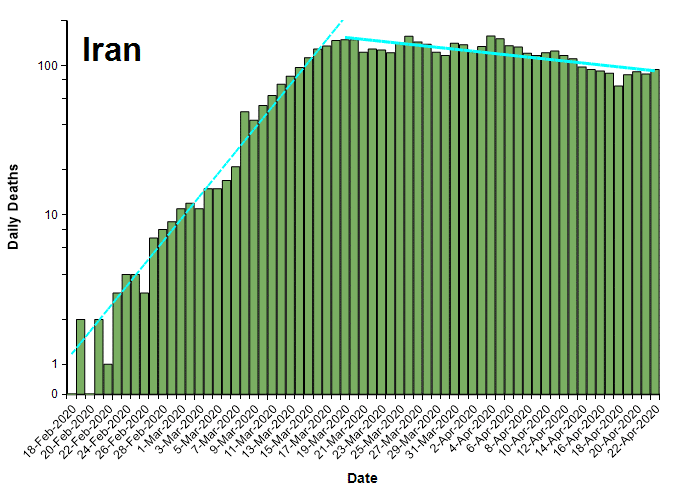
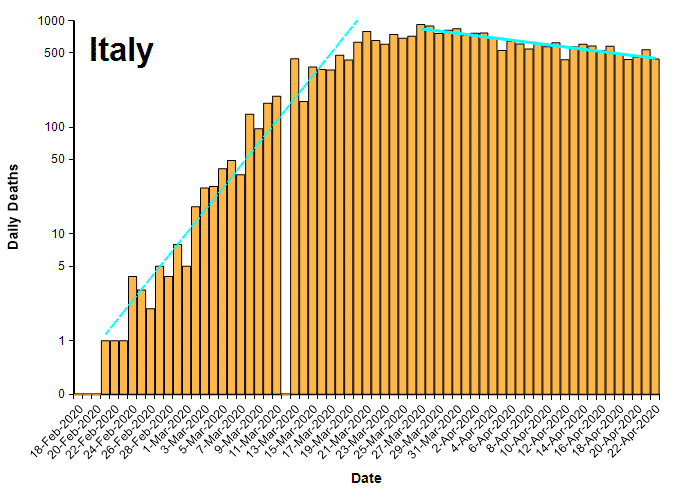
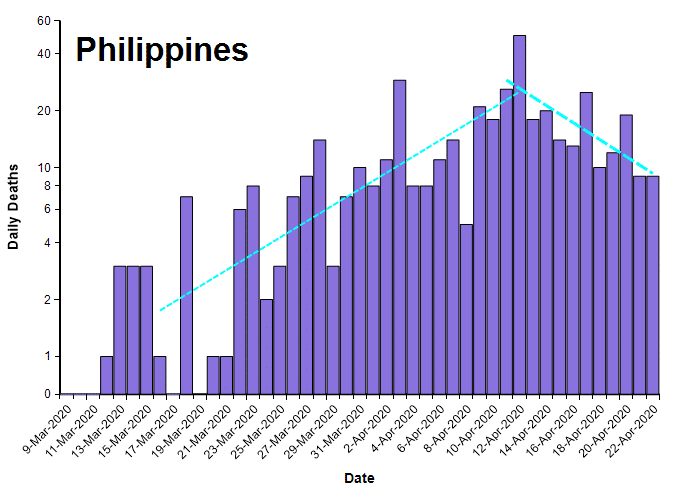
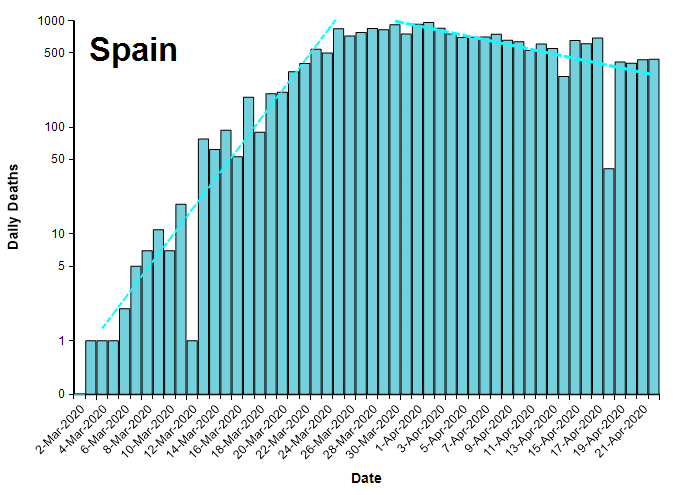
It is worth mentioning that the number of deaths per day is already below half of their peak rates for these countries (except Iran), which by any measure is a big improvement. On a linear Y scale, a reduction to 1/2 the peak rate looks dramatic, as seen in the same data for Spain shown here with a linearly-scaled Y axis.
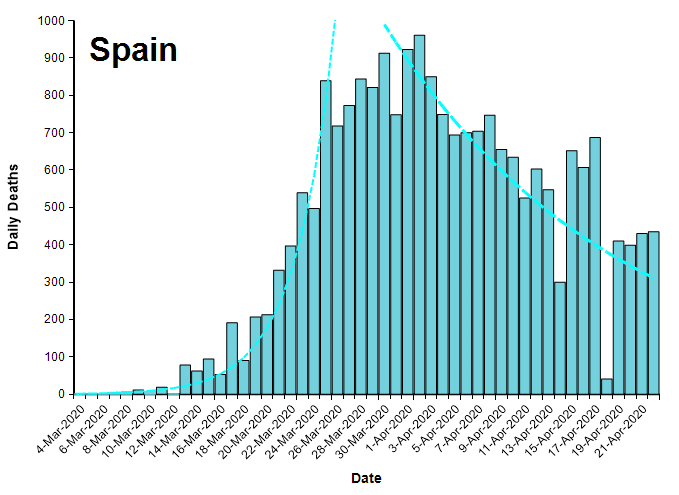
Comparison of growth and decay rates
The following table compares the daily growth and decay rates for each country. The Growth/Decay column shows the ratio of the growth rate to the decay rate. Currently, the recovery rate varies from half the growth rate (in China) to 1/13th as fast (Iran). The final Date suppressed column shows the date when the decay trend line crosses the ten deaths per day level.
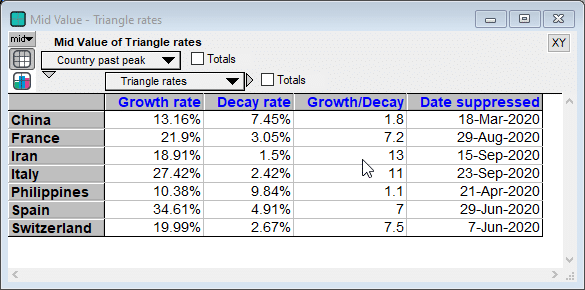
Summary
The exponential decay rate during recovery gives us an indication of how long the recovery phase will last, assuming today’s level of lock down measures remain in place. The decay rate may improve with medical breakthroughs, tighter lock downs, high levels of immunity, or altered societal behaviors. They may get worse, or even reverse, with loosing of social distancing measures.
With the exception of China, all the countries shown here appear to have barely crossed the peak. The apparent decay rates as of today are preliminary given that these countries have not been past the peak for very long.
References
- [C20a] Chrisman, Lonnie (23-Mar-2020), “Suppression strategy and updated forecast for US deaths from COVID-19 Coronavirus in 2020“, Lumina.com blog.
- [C20b] Chrisman, Lonnie (15-Apr-2020), “A critique of the HealthData.org COVID-19 model, and how it works“, Lumina.com blog
- [H20] Henrion, Max, “The Suppression Triangle for COVID-19: How soon can we end the lockdown?“, Lumina.com blog
- [IMHE20] IHME COVID-19 health service ulitization forecasting team (26 March 2020), “Forecasting COVID-19 impact on hospital bed-days, ICU-days, ventilator days and deaths by US state in the next 4 months“, MedRxiv. doi:10.1101/2020.03.27.20043752.
- [JH20] John Hopkins University Center for Systems Science and Engineering (JHU CSSE), “2019 Novel Coronavirus COVID-19 (2019-nCoV) Data Repository by Johns Hopkins CSSE“, GitHub data repository.